店舗

店舗情報トップ

本日の打ちいこ情報

機種

機種情報トップ

新台カレンダー

設定判別ツール

演出信頼度まとめ

新台レポート

コンテンツ

コンテンツトップ

特集記事

マンガ

動画

お知らせ

コミュニティ

自由帳

マイページ

パチポイント

スロッコ

歴代人気投稿

【ネタ】収束までの道のり

メニュー

★フリーテーマ | コラム

【ネタ】収束までの道のり

ebotanさん: 投稿日：2019/07/02 15:35

ebotanです。

確率の収束について、そういえば実際にコード書いてコラムにした人いないなぁと思ったので適当ですが書きました。
よく「パチンコ/パチスロの確立は1日回しても収束しない」と言ったものですが、文章で長々書いてもわかりにくいので数字で出しちゃえという思いつきです。
ちなみに実機に実装されている乱数生成の仕組みと全く違うので、あくまでも確率の収束に焦点を置いて頂けるとありがたいです。

※過去コラムを簡単にしか漁ってないので内容被ってるコラムがあるかもしれませんが...

- まず言い訳
実際はどうだとか計算的にはとかアルゴリズムだとかコードの綺麗/汚い等は全く考えてないのでご了承ください。
また、名誉のために申し上げますが本業はハードウェア設計ですのでPerlは初心者に毛が生えそろったぐらいしか書けません。

- ソースコード

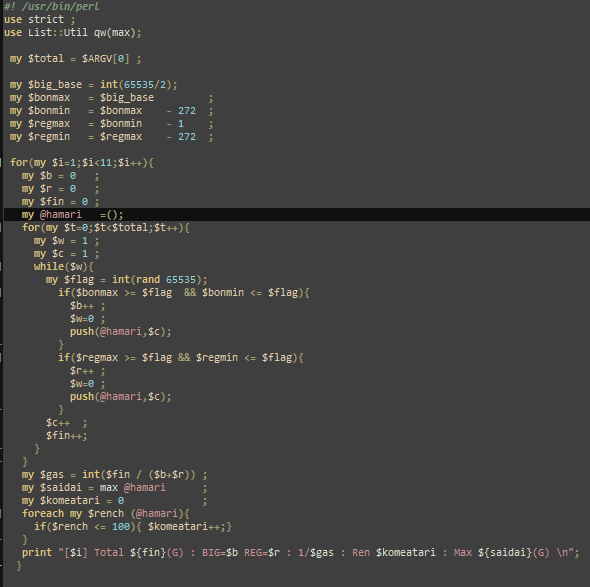
{Photo01}

- 仕様
・ボーナスを特定回数引くまでぶん回す、というのを10回繰り返すプログラムです。
・Perlの処理には時間概念がないのでrand関数を使用して疑似乱数を生成しています。
・ボーナス確率はマイジャグラー4を参考に、BIG:1/240、REG:1/240、合算1/120を想定しています。小数点以下はめんどくせぇので全部切り捨てです。
・当否判定はrand関数で生成される0〜65535までの65536個の数字の内、32767〜32495をBIG、32494〜32222をREGとして判定します。

- 余談
本当はハードウェアで16bitカウンタを作り、不規則なタイミングでカウンタ値を取得し、あらかじめ用意した当否テーブルを参照する方が実機っぽいんですが、面倒ですしシミュレーションするのに時間がかかるためあきらめました。乱数生成ICの仕様を知らないのでガチガチに作ってもなぁとも思ってます。

さて、前置きはそこそこにして本番行ってみましょう。ちなみにいずれの結果もぶっつけ本番です。

- 結果の見方
[回数] 総G数 : BIG回数 REG回数 : 合算 : 100G以内の当選回数　: 最大ハマり

- 結果
◆ボーナス１回

{Photo02}

まぁ、1回目はこんなものでしょう
一番ハマったのは[2]の431G、一番早かったのは[10]の4Gでの当選になります。
朝イチ400G以上のハマりとか勘弁してほしいです。

◆ボーナス10回

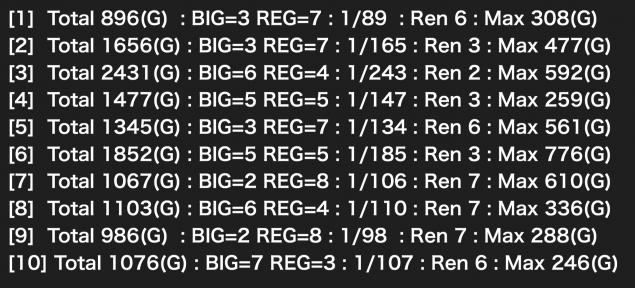
{Photo03}

確率的にはまったく収束しておらず、合算値もBIG/REG比率もバラバラです。
10回当たるまでの総ゲーム数も最小値896G、最大値2431Gとかなり差があります。

◆ボーナス30回

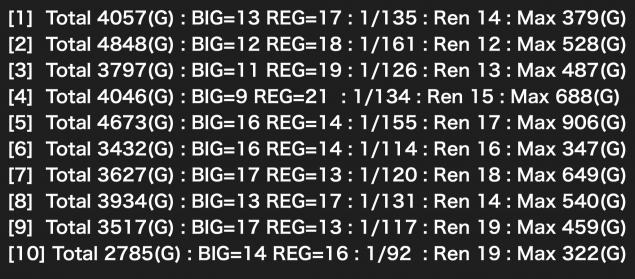
{Photo04}

[10]は総G数が少なく、100G以内の当選数は多い、さらに最大ハマりも322Gと非常に優秀です。
一番しんどいのは[4]ですね...プログラムの実行結果なのに確率を疑いたくなります。
とはいえ、ボーナス30回程度でもまだまだバラバラなのは見てわかる通りです。

◆ボーナス60回

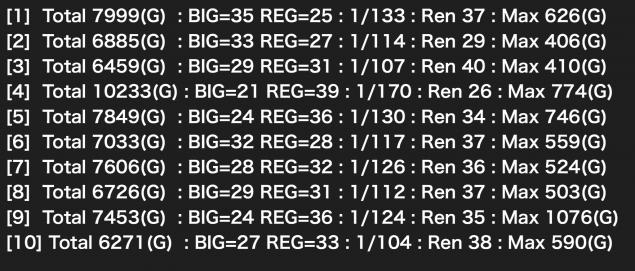
{Photo05}

ボーナス60回と言ったら都内ですと終日ぶん回した結果になると思われますが、全然バラバラです。
[4]のような恐ろしい結果も全然ありえるということで、終日ぶん回しても収束しないというのがよくわかります。

◆ボーナス100回

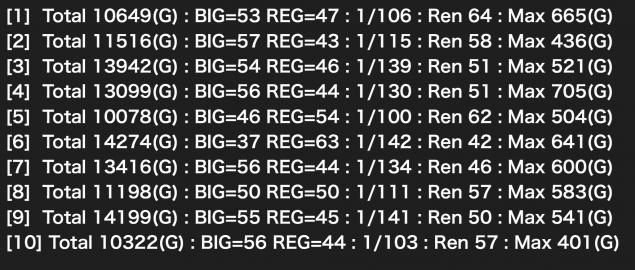
{Photo06}

お盆/年末年始の延長営業でいけるか/いけないかギリギリの回数ですね。
でも、まだバラけてます。収束にはほど遠いようです。

◆ボーナス500回

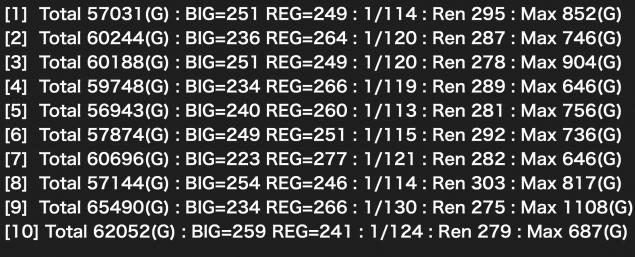
{Photo07}

ぼちぼち異次元的な回数に突入しますが、まだ想定している確率には収束してくれません。
BIG/REGの確率は収束が見えなくもないですが、うーん...

◆ボーナス1000回

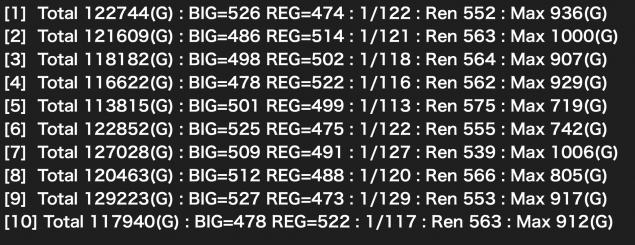
{Photo08}

4桁に突入しました。
[9]がちょっとアームザコ気味ですが、合算値のバラつきが大人しくなりました。

◆ボーナス5000回

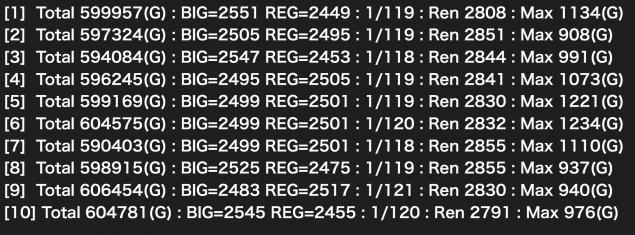
{Photo09}

合算値がほぼほぼ収束しました。
想定の1/120の誤差範囲と言ってもいいかなって結果です。

◆ボーナス100000回

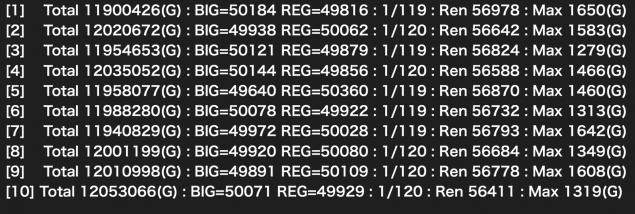
{Photo10}

これはもう収束したと言っていいでしょう(飽きた)
総ゲーム数が軒並み一千万を超えてるのが異次元的で素敵ですね。

- おまけ

◆PGG(1/8192)１回 Version

[1] Total 167(G) : PGG = 1 : 1/167
[2] Total 4698(G) : PGG = 1 : 1/4698
[3] Total 12163(G) : PGG = 1 : 1/12163
[4] Total 8(G) : PGG = 1 : 1/8
[5] Total 50636(G) : PGG = 1 : 1/50636
[6] Total 29468(G) : PGG = 1 : 1/29468
[7] Total 18437(G) : PGG = 1 : 1/18437
[8] Total 4578(G) : PGG = 1 : 1/4578
[9] Total 3109(G) : PGG = 1 : 1/3109
[10] Total 9445(G) : PGG = 1 : 1/9445

[4]、お前...?